数据大佬:模型下的最优无限火球任务法卡组

大佬UbpaX用数据为我们解析最优的无限火球任务法卡组，卡组在文章最后。

一. 模型

卡组 deck：30张，相对顺序不发生改变

额外法术：除宝典外套牌之外的法术(或者随从)，如魔典，雕文，共鸣，鬼隐巫师等

条件1：至少1个巫师学徒，1个大法师，模拟幻影熔岩镜像和另一个巫师学徒总数不少于 3

条件2：( 1个宝典和至少3个额外法术) 或 2个宝典

最后一个key牌的位置 lastKeyIdx：能满足条件 1 和条件 2的牌库的前 n 张牌，n 中的最小值为 lastKeyIdx

过牌：能让你从牌库抽牌的各种机制。这个是核心概念，下面重点说明。

1. 简单的抽牌和滤牌：大哥，奥数智慧，工程师学徒，秘法学家等

2. 苟活牌：苟活牌实际上并不抽牌，但苟活的一回合能让你多抽一张牌，如冰箱，冰环，暴风雪，末日等

3. 任务奖励：做完任务的一回合能抽 1 张牌

4. 硬抗：30点血量能换来的回合数，只考虑前期，后期情况一律认为无法硬抗，默认是前期是前 4 回合，即前1-4回合可以不依赖任何苟活牌活下去

5. 起手：先手3张后手4张，平均 3.5 张

这里我一开始分析时陷入了一个误区，就是不知道如何统一 过牌，苟活和每回合固定的1张抽牌

我的方法是：把一切每回合固定过牌都认为是自己争取来的，包括硬抗的4张，苟活牌带来的 n 张，任务奖励带来的 1 张，起手的3.5张

过牌的分级：显然在上述过牌的概念里边，不同的过牌的地位显然是不同的，具体分析很有必要

1. 固定过牌：8.5张 = 硬抗 4 张 + 起手 3.5 张 + 任务奖励 1 张

2. 稳定过2张牌：奥数智慧，大哥

3. 稳定过1张牌：冰箱，工程师学徒，战利品，血法，侏儒发明家等

4. 期望过2/3牌：秘法学家(经过计算，2秘法3奥秘期望过大约 0.65张/秘法学家，1秘法2奥秘期望过 0.67张/秘法学家 )

5. 1级衰退过牌：冰环，暴风雪(前期摸到基本能争取1回合，越到后期能争取的回合越少)

6. 2级衰退过牌：末日，冰甲，冰锥(前期摸到基本能争取1回合，越到后期能争取的回合越少，相比1级衰退更严重，虽然末日的机制有些许不同但期望效果类似)

在第 lastKeyIdx 张能过的牌数：将牌库中第 lastKeyIdx 张前的牌称为 手牌

能过的牌数 = 固定过牌 + 手牌的稳定(期望)过 2/3, 1, 2牌 + 衰退函数(手牌的1级衰退过牌)+ 2/3 * 衰退函数(手牌的2级衰退过牌)

(衰退函数呈 S 型，依经验而定，2级衰退的系数 2/3 依经验而定)

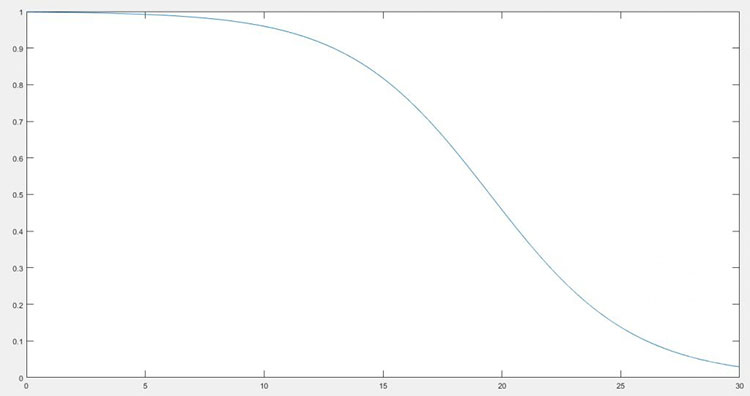
能获胜：一开始定义为在第 lastKeyIdx 张能过的牌数 不少于 lastKeyIdx，而实际情况是有一定概率发挥出较好的过牌水平(成功达成末日冰环，雕文找到过牌单解aoe等)，因此将牌数 少于 lastKeyIdx的情况也考虑在内

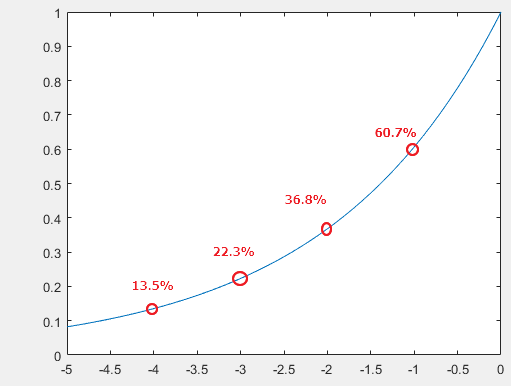
前者100%能获胜，后者获胜概率依经验定义为 e^( 牌差/2)，具体曲线如下

根据经验至少得含有的牌(共25张)

二. 模拟

!!!胜率越接近实际说明模型越能反应实际情况，胜率越高说明在相对意义下在此模型内卡组越好!!!

用数字代表卡牌

0：任务

1：巫师学徒

2：熔岩镜像

3：模拟幻影

4：额外法术

5：宝典

6：大法师

7：稳定过2张牌的牌

8：稳定过1张牌的牌

9：期望过2/3张牌的牌(秘法学家)

10：1级衰退过牌

11：2级衰退过牌

模拟过程如下

1. 卡组就表示为有11个元素的数组，如 [2, 2, 1, 1, 2, 2, 4, 8, 1, 4, 2]，第 i 个元素的值代表数字 i 的卡牌的张数

2. 那么一个牌库样本就表示为有先后顺序的有30个元素的数组，如 [0, 10, 5, 10, 11, 8, 8, 1, 8, 8, 9, 7, 8, 6, 7, 8, 8, 6, 2, 1, 2, 10, 8, 5, 7, 4, 7, 8, 10, 11]，任务必定在第一张

3. 从牌库样本可以计算得到 lastKeyIdx，上例中其为 26

4. 从而可算出在第 lastKeyIdx 张能过的牌数，上例中其为 26.1224

5. 从而可判断出能否获胜(或者是获胜的概率)，上例中说明定义层面上 100% 获胜

6. 重复2-5步骤，记录其中获胜的次数，从而可计算出模拟的平均获胜概率

三. 实验结果与分析

根据经验，先明确卡组中各元素最小值，为 [ 2, 2, 1, 1, 2, 2, 4, 4, 1, 3, 2]，就是上面所提到的必须卡

1. 首先来测试我自己的卡组，为 [2, 2, 1, 1, 3, 2, 4, 4, 2, 4, 4]，经过模拟，得出的结果意外地好，就是49%，从数值上看很合理，说明所建模型能较好地反应实际的卡组胜率情况

2. 其次探究额外法术 3 张，4张，5张给卡组带来的变化，以我的卡组为标杆进行转变

[2, 2, 1, 1, 4, 2, 4, 4, 2, 4, 3] : 48.0% // 1 个过牌(冰锥) 换 额外法术

[2, 2, 1, 1, 5, 2, 4, 4, 2, 4, 2] : 44.2% // 2 个过牌(冰锥,冰甲换共鸣) 换 额外法术

[2, 2, 1, 1, 5, 2, 4, 4, 2, 3, 3] : 41.3% // 2 个过牌(暴风雪冰锥) 换 额外法术

[2, 2, 1, 1, 6, 2, 4, 4, 2, 3, 2] : 37.3% // 3 个过牌(暴风雪冰锥,冰甲换共鸣) 换 额外法术

从以上可以看出，用较低劣的过牌去换取更多的额外法术实际上降低了胜率，因此得出结论：过牌对卡组的影响大于额外法术

这让人感到很意外，毕竟额外法术越少，那抽齐6张法术的难度会上升很多，但胜率反而提高了

3. 尝试将 1张额外法术(魔典)换成稳定1张过牌

[2, 2, 1, 1, 2, 2, 4, 5, 2, 4, 4] : 55.6% 1 法术(魔典) 换 稳定1张过牌

胜率竟然意外的提高了。少了一张额外法术，意味着必须要抽齐2张宝典才能做完，这使得宝典成为了必须摸到的 key 牌。

4. 总结 2 和 3 的情况

为了 [定性] 地解释以上2个情形，我特地模拟求出了 lastKeyIdx 的期望值，结果为 25，这意味着大部分情况(大概为60%)需要摸25张，此时摸到双宝典概率大概为 69.5% ≈ (25/30)*(25/30)，当情况为 26, 27, 28, 29 时，摸双宝典的概率会更接近 1

这也就是说 额外法术与过牌的权衡中，过牌带来的受益会更高(一方面提高了摸key牌的概率，另一方面也提高了摸宝典的概率)

5. 考虑尽可能大的过牌量

[2, 2, 1, 1, 2, 2, 4, 8, 1, 4, 2] : 77.2% 魔典, 冰锥, 冰甲, 秘法学家 换 过牌

根据 4 的结论指导，通过尽量增加过牌量，使得模拟下的胜率更高了，当然数值可能有点脱离实际了，但其数值在相对意义上是有价值的

6. 增加一张模拟幻影，以实验 5 的卡组为标杆

[2, 2, 2, 1, 2, 2, 4, 7, 1, 4, 2] : 66.5% 1 过牌 换 模拟幻影

多一张模拟幻影，虽说集齐 key 牌更加容易，但也降低了卡组过牌的流畅性，相比 5 来说胜率下降是意料之内的

四. 总结

1. 经验上需要至少保证3张额外法术并不是必要的，只靠双宝典并不会明显影响达成条件1和条件2的概率

2. 期望上看一场对局需要过上25张牌

3. 将一张过牌换成 多一张的模拟幻影 并不能带来稳定性的提升，实际上降低了过牌流畅性

4. 1个秘法学家2个奥秘和2个秘法学家3个奥秘从期望上来说过牌效率是几乎一样的

5. 过牌对卡组的胜率(模型下)是显著的

五. 模型下最优卡组

依据实验 5 对卡组进行构筑，样例如下

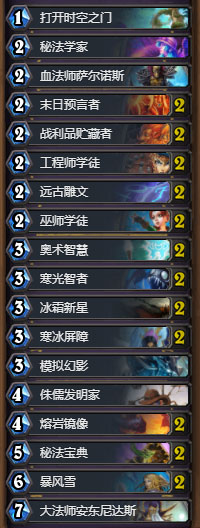
卡组代码：AAECAf0EBrQC7QW4CMHBAtDBArnRAgyKAcAB+wGcAskDqwTLBOYE+AeSrAKYxALaxQIA